CPA Angriff auf Speck
Robin Dietrich & Marius Schwarz
Agenda
- Speck Schiffre
- CPA Angriffe
- CPA auf Speck
- Gegenmaßnahmen
- Hiding
Speck
- Symmentrische ARX Schiffre
- Add/Rotate/XOR
- Entworfen von der NSA (Zusammen mit der Schiffre Simon)
- Performant in Hard-/Software
- Speck bietet mehrere mögliche Modis
- Anzahl Runden, Schlüssellänge, Blocklänge
- Paper: Simon and Speck: Block Ciphers for the Internet of Things
Speck - Setups
| Speck | Blocklänge | Schlüssellänge | Runden |
|---|---|---|---|
| Speck3264 | 32 Bit | 64 Bit | 22 |
| Speck4872 | 48 Bit | 72 Bit | 22 |
| Speck4896 | 48 Bit | 96 Bit | 23 |
| Speck6496 | 64 Bit | 96 Bit | 26 |
| Speck64128 | 64 Bit | 128 Bit | 27 |
| Speck9696 | 96 Bit | 96 Bit | 28 |
| Speck96144 | 96 Bit | 144 Bit | 29 |
| Speck128128 | 128 Bit | 128 Bit | 32 |
| Speck128192 | 128 Bit | 192 Bit | 33 |
| Speck1281256 | 128 Bit | 256 Bit | 34 |
Speck - Rundenfunktion
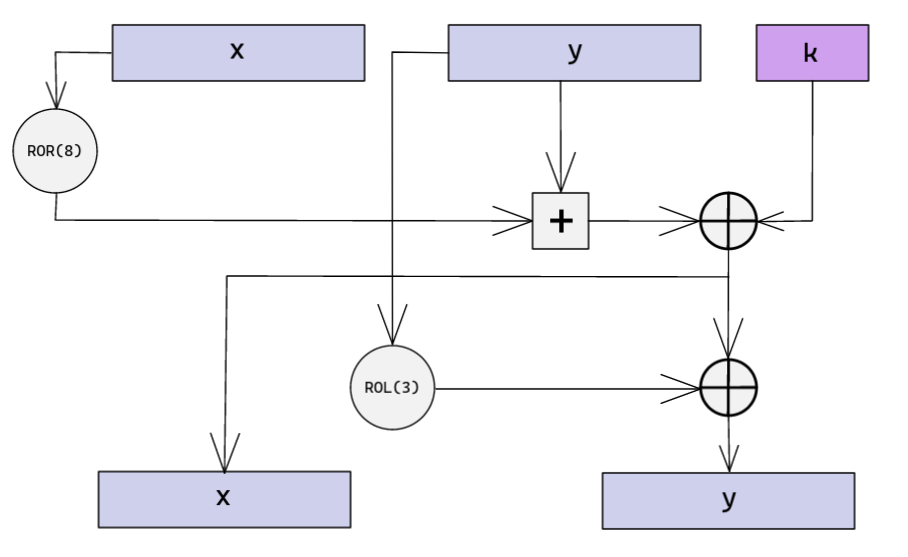
- Wird während der Key Schedule aufgerufen
- Wird beim der Verschlüsselung aufgerufen
Speck - Pseudocode
pt = Plaintext Bytes Pt = Plaintext as 16 Bit Words
ct = Ciphertext Bytes Ct = Ciphertext as 16 Bit Words
k = Key as Bytes K = Key as 16 Bit Words
// Key Schedule
D=K[3], C=K[2], B=K[1], A=K[0]
for i in 0..<22
rk[i]=A
ER16(B, A, i++)
rk[i]=A
ER16(C, A, i++)
rk[i]=A
ER16(D, A, i++)
// Encryption
Ct[0]=Pt[0]; Ct[1]=Pt[1];
for i in 0..<22
ER16(Ct[1], Ct[0], rk[i++])Speck - Möglicher Angriff
- Angriff der Rundenfunktion
- ADD/XOR/ROT Operationen
Speck - Möglicher Angriff
- Der Rundenschlüssel steckt in der XOR Operation:

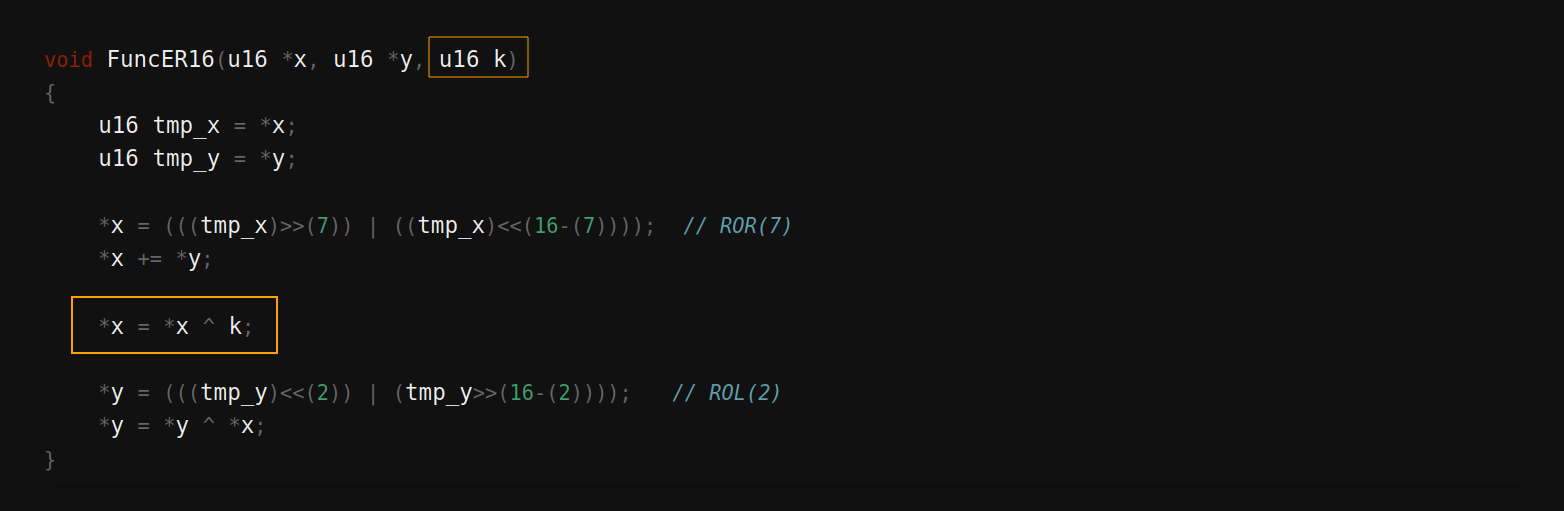
Correlation Power Analysis
- Variante von Differential Power Analysis (DPA)
- Nutzt Pearson Correlation Coefficient (PCC)
- Bei Speck: Korrelation zwischen Power-Trace und Rundenschlüssel
- Vorgehen:
- Modell erstellen
- Finden der Korrelationen im Modell
- Anwenden auf Hardware Implementierung
Hamming Weight
- Passendes Modell zum ‘bewerten’ des Stromverbrauchs
- Chip hat ein gewissen Basisverbrauch (IDLE)
- Werden Bytes im Chip verändert (0 → 1; 1 → 0) wird Strom benötigt
- Verhalten kann durch die Hamming-Distanz simuliert werden
- Hamming Distanz: Anzahl der Veränderter Bits:
HammingDistance(0100101,0010101) = 2
Der Unterschied zweier per XOR verknüpfter Daten, wird als Hamming-Gewicht bezeichnet:
HammingDistance(0100101,0010101) = HammingWeight(0100101⊕0010101)
Speck - Modell
- Einfaches Modell der Speck Verschlüsselung
- Kann für die ersten 2 Byte des Rundenschlüssels genutzt werden:
Speck - Simulation
- Simulation anhand des Modells mit n traces
- Generieren von n zufälligen Klartexten mit fixem Keybyte (+ noise)
- Simulation aller möglichen Keybytes per Hamming Weight
- Berechnen des PCC aller Keys über alle traces
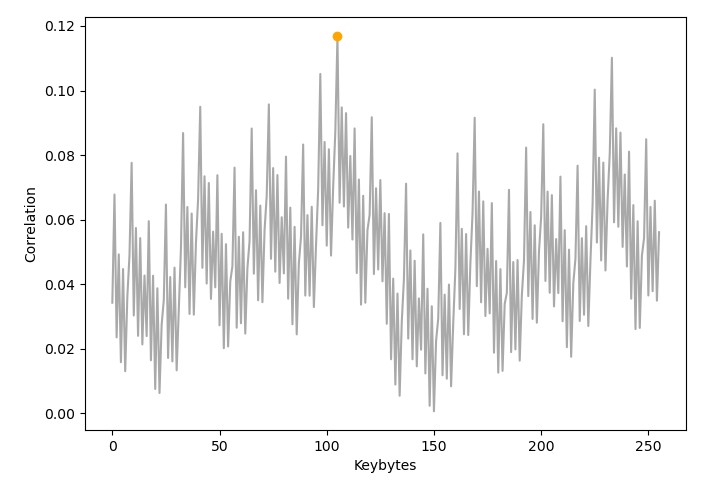
→ Das korrekte Keybyte ist: 0x68
T-Test
- Wird verwendet um Leakage zu erkennen
- Gibt das Berechnen einer Chiffre mehr Information zurück als geplant: Leakage
- Ausnutzbar z.B. durch die Power Traces
- Berechnet durch:
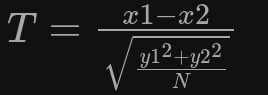
- Vergleicht zwei unabhängige Stichproben miteinander, und vergleicht Mittelwerte
- Je unterschiedlicher die Mittelwerte → desto weniger Leakage
T-Test
- T-Test der aufgezeichneten Power-Traces:
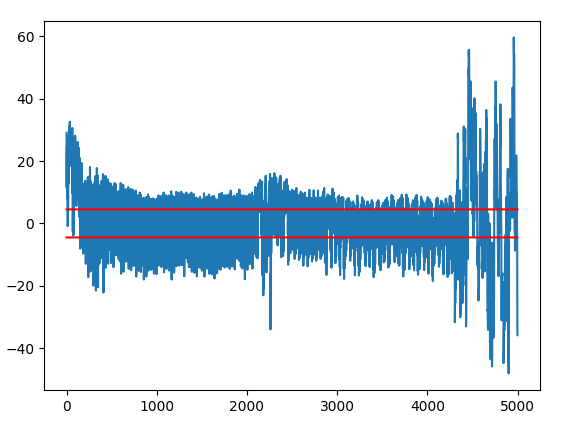
Angriff - Hardware
- Implementierung von Speck auf CW
- Aufzeichnen von n Power Traces
- Berechnung des Software Modells
- Berechnen der Korrelationen zwischen Modell/Powertraces
- Keybyte für Keybyte
- Rückrechnen des Rundenschlüssels
Korrelationen des ersten Keybytes
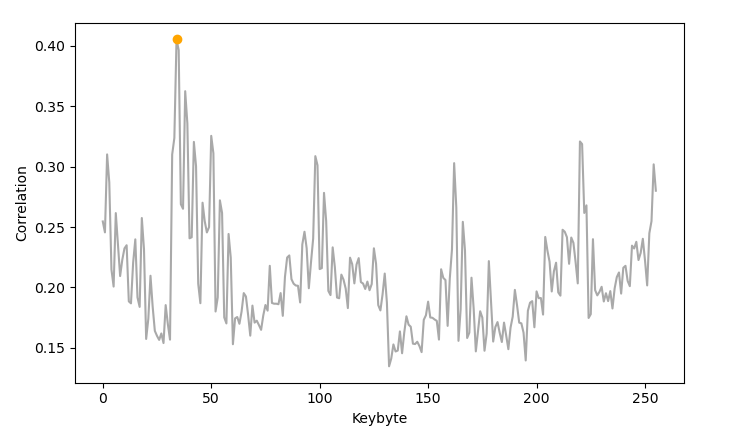
- Correlationen des ersten Keybytes
- Korrelation fällt höher aus als im Modell
- Deutliches Maximum der Korrelation bei 0x22 (Korrektes Keybyte)
Problem: Blocksize
- Bei Speck1632: Operationen nicht auf Byte sondern auf 16-Bit Ebene
- Erste Idee: Modell und Korrelation auf 216 Keys
- → Keyspace ist abdeckbar (65536 Keys)
- → Zu langsam, Unschön
- → Nicht möglich für andere Modis von Speck (32 Bit Subkeys)
- Lösung: Modell funktioniert auch auf allen Teilbytes per Shift:
rightkey = 0x00
for guess_key in range(256):
leftkey = model( (guess_key << 8) + righkey )
for guess_key in range(256):
rightkey = model( (leftkey << 8) + guess_key )- Auch umsetzbar auf Speck mit Blocksize > 16 Bit
Problem: nth Keybytes
- Modell kann nur für die ersten zwei Keybytes genutzt werden, da:
- Die (bereits bekannten) Rundenkeys müssen miteingeschlossen werden
- Muss an der richtigen Stelle passieren (⊕-Operation)
Problem: nth Keybytes
- Anpassung des Modells:
# -------------- for one key -----------------#
x = ((x << (16 - ALPHA)) + (x >> ALPHA)) & mod_mask # x = ROR(x, 7)
x = (x + y) & mod_mask # x = ADD(x, y)
x = x ^ knownkey[0]
# -------------- for second key -----------------#
y = ((y >> (16 - BETA)) + (y << BETA)) & mod_mask # y = ROL(y, 2)
y = y ^ x # y = XOR(y, x)
x = ((x << (16 - ALPHA)) + (x >> ALPHA)) & mod_mask # x = ROR(x, 7)
x = (x + y) & mod_mask # x = ADD(x, y)
x = x ^ knownkey[1] # x = XOR(x, k)
# -------------- for third key -----------------#
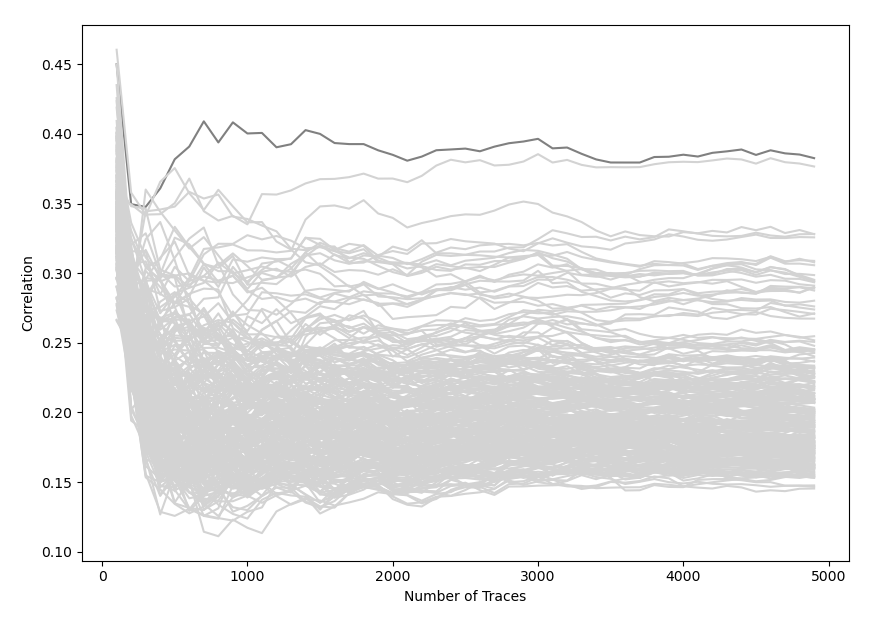
# [...]Korrelationen des ersten Keybytes
- Graph zeigt die Korrelationen des ersten Keybytes bis 5000 traces
- Ab ~800 Traces hebt sich die Korrelation deutlich hervor
Gegenmaßnahmen
Hiding
- Verstecken des eigentlichen “Leakages” in Rauschen
- → Erhöhung des vorhandenen Rauschens während der Berechnung
- Mehrere Möglichkeiten
- Mischen der Instruction-Order
- Hinzufügen von “Dummy Instructionen”
- Clock Jitter
Hiding - Code
- Ansatz: Korrelation kommt von
ER16()- Add/XOR/Rotate
- Hinzufügen weitere AXR Operationen um noise zu erhöhen
- Ersetzen von jeder XOR Operatione mit folgender:
uint16_t XOR(uint16_t a, uint16_t b, int random) {
uint8_t tmp = random ^ 0x5F;
tmp ^= (random ^ a);
tmp ^= (tmp ^ b);
tmp &= (tmp & a);
tmp &= (tmp & b);
return a ^ b;
}Randomwird bei jeder Verschlüsslung erneut generiert
Hiding - T-Test
- Ergebnisse des T-Tests mit implementierter Hiding Maßnahmen:
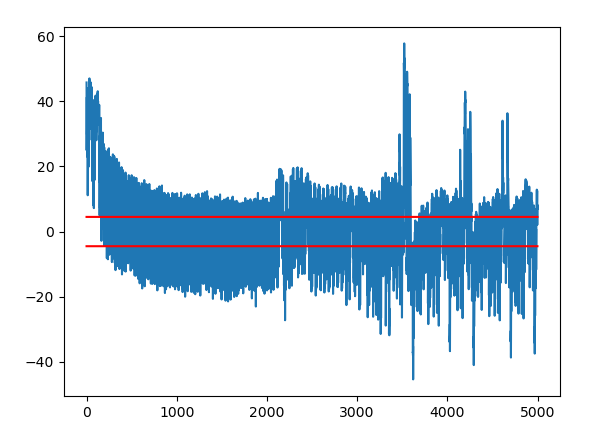
- Bedarf weitere Analysen, Unterschied der beiden T-Tests sind nur Minimal
- Keine Indikation dass Hiding funktioniert laut T-Test
Korrelationen des ersten Keybytes
- Besseres Ergbniss der Korrelationen bis 5000 Traces
- Korrelationen flachen ab ~800 drastisch ab
- Keine Korrelation sticht heraus
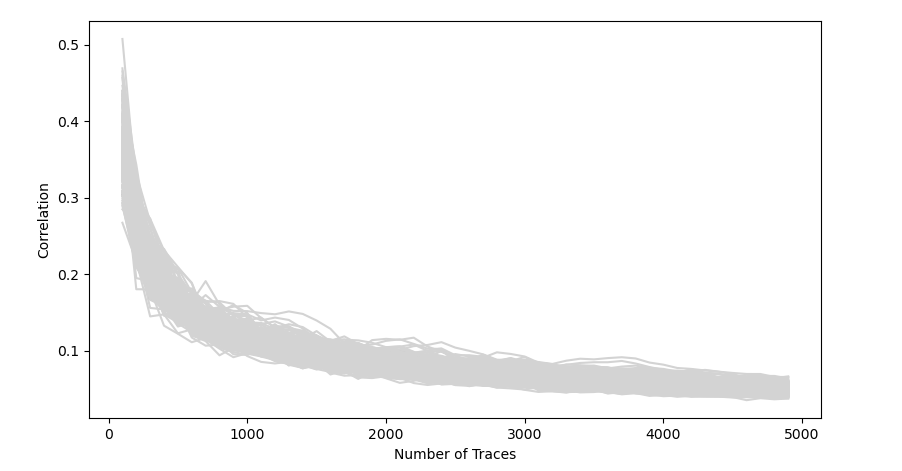
- Es war nicht möglich den Angriff erneut durchzuführen
- Neue Korrelationen nach einigen Test lediglich bei ~0.18 mit falschem Keybyte
Hiding (Potentieller) Bypass
- Korrelation sollte weiterhin möglich sein wenn man die Operationen in Betracht zieht
- Schwierigkeit hängt am Zufallszahlengenerator
- Problem: Sichere Zufallszahlen auf Embedded Chips ist nicht trivial
→ Bypass konnte nicht realisiert werden